In the previous post, I said that when you ask a waiter “Is [some dish] vegan?” you would not want to hear the answer “I don’t know”.

But what if you ask about a dish that they do not serve? Imagine asking “Are Powidltatschkerln vegan?” somewhere outside Austria. I would totally expect to hear “I don’t know” as an answer. (They are not, by the way).

So, we might need a boolean with a third “I don’t know” option, after all…

Union Types

At the end of the previous part of this series, I turned on “strict” type checking. That setting removes null and undefined from the possible values for all types (and it does more).

I would argue that this is the better default behavior for new projects. Without strict null checks enabled, null and undefined are part of every set and one cannot remove them. When we turn on strict, null and undefined are removed from every set—but we can bring them back:

//use directly:
const vegan : boolean | null = null

//...or define a type alias
type NullableBoolean = boolean | null
const glutenFree : NullableBoolean = null

The | here looks like the “logical or” operator of JavaScript—and you should also read it as “or”. So, vegan is a variable that is either a boolean or null and by defining the type alias NullableBoolean we get a type that is a boolean or the value null.

Intersection Types

What if we use & instead of |? Can we do that too?

type NullableBoolean = boolean | null
const n : NullableBoolean = null

type MaybeDefinedBoolean = boolean | undefined
const m : MaybeDefinedBoolean = undefined

type Intersection = NullableBoolean & MaybeDefinedBoolean
const u1 : Intersection = true
const u2 : Intersection = false
const u3 : Intersection = null //ERROR
//Type 'null' is not assignable to type 'boolean'.(2322)
const u4 : Intersection = undefined //ERROR
//Type 'undefined' is not assignable to type 'boolean'.(2322)

Here we get a new type Intersection that is both a NullableBoolean and a MaybeDefinedBoolean.

Every value of that type must satisfy all restrictions of NullableBoolean and all restrictions of MaybeDefinedBoolean. And there are only two values that are both

• boolean | null and also
• boolean | undefined

at the same time: Only the values true and false satisfy both restrictions.

Back to Sets

When I first learned about union and intersection types (in another type system, a few years ago), I could not remember why “and” is and “intersection” while “or” is a “union”. The word “and” always sounded like it would add something, so when I thought of “and”, I also thought of “union”. Which is wrong, of course.

For me, it became easier to distinguish the names when I learned to think about the sets of possible values.

When a variable can hold either values from one type or values from another type, the set of possible values for this variable is the union of the other two sets.

Our NullableBoolean can hold values from boolean or from null, so the set of possible values is the union of boolean and null.

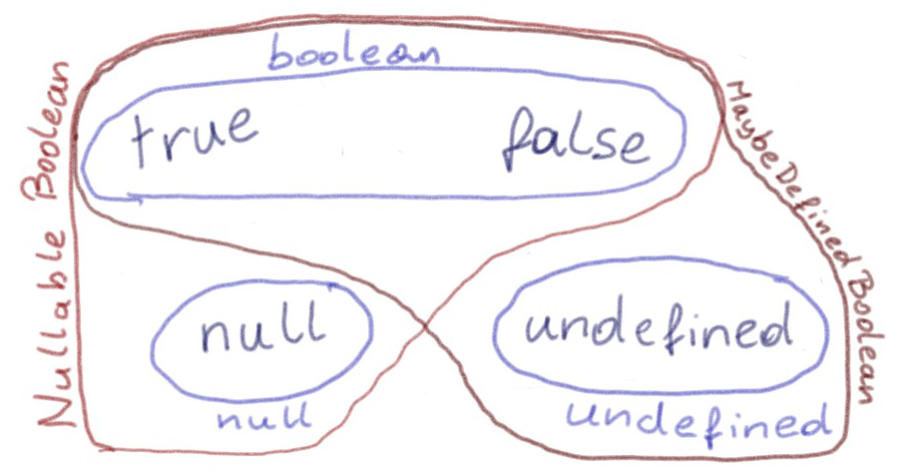
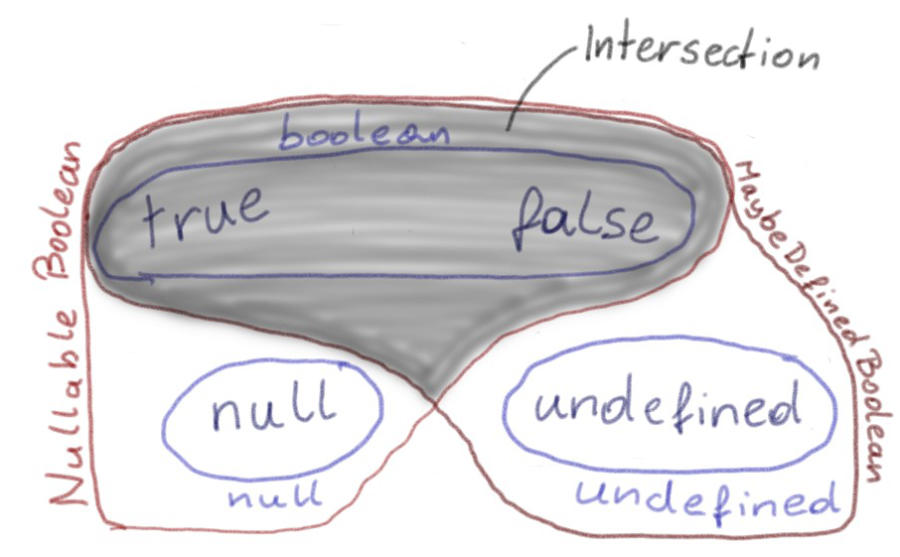
When, on the other hand, a value for a variable must satisfy all requirements from two or more types, the set of possible values for this variable must come from the intersection of the other sets.

Our type Intersection must both be a NullableBoolean and a MaybeDefinedBoolean at the same time, and the only two values in this intersection of the two sets are the “original” boolean values true and false.

Conclusion

Union types (A | B) allow us to define types where the possible values are of either one type or another type. The possible values come from the union of the original sets. One simple thing we can do with unions is add more possible values (like null or undefined) to an existing type.

Intersection types (A & B) allow us to combine the restrictions of different other types. The possible values come from the intersection of the original sets. One simple thing we can do with them is remove possible values from an existing type.

I will get back to unions and intersections again in later posts—because one can not only use them toadd null or undefined to a type in strict mode, but do more interesting stuff with them.